
Quantum states can be represented by vectors belonging to a so-called Hilbert space. Vectors provide an ideal framework to represent statistical regularities, especially when incompatible observables are involved. To see how this works, let ![]() be a vector of unit length in the plane and consider its projections on two orthogonal axes
be a vector of unit length in the plane and consider its projections on two orthogonal axes ![]() and
and ![]() (figure 5). The Pythagoras' theorem entails:
(figure 5). The Pythagoras' theorem entails:
Now suppose that we measure an observable A that can only take two values, ![]() and
and ![]() . The probabilities of getting
. The probabilities of getting ![]() and
and ![]() vary depending on the way the measured system has been prepared.
vary depending on the way the measured system has been prepared.
Nevertheless, since ![]() and
and ![]() represent mutually exclusive occurrences exhausting the spectrum of the possible outcomes, we know a priori that the corresponding probabilities meet the condition :
represent mutually exclusive occurrences exhausting the spectrum of the possible outcomes, we know a priori that the corresponding probabilities meet the condition :
The predictive formalism of quantum theory is based on the parallelism between eq. (1) and (2). It is sumarized by the following rules:
I. The values ![]() that an observable A can take are represented by orthogonal axes
that an observable A can take are represented by orthogonal axes ![]() spanning a state space.
spanning a state space.
II. Each experimental procedure which ‘prepares' a system before a measurement of A is represented by a state vector ![]() belonging to the state space and having unit length.
belonging to the state space and having unit length.
III. (Born rule) If we measure the observable A, the probability ![]() to get the value
to get the value ![]() is given by the modulus squared of the projection of
is given by the modulus squared of the projection of ![]() on the
on the ![]() axis:
axis: ![]()
We have been concerned so far with a special class of observables, namely those observables that can be represented by different orthogonal frames within the same state space. The probability distributions associated with such observables are rigidly connected to one another. In the case of Sz and Sx, for instance, we have seen that, given an equiprobable distribution of ‘up' and ‘down' for Sx, the statistics of Sz necessarily follows one of the two distributions represented in figure 7.
However, there exist observables whose respective probability distributions are a priori completely independent. A typical example is provided by the spin observables of two distinct particles. Particle 1 can be prepared in such a way that ![]() and particle 2 in such a way that
and particle 2 in such a way that ![]() . (This cannot be done if Sx and Sz are measured on the same particle, since Sx and Sz are incompatible observables.) In general, however, once two quantum systems have interacted, they become correlated in such a way that measurement results can no longer be anticipated by just assigning an individual state vector to each partner. Instead, a unique, global state vector has to be associated to the whole pair. This state is constructed by combining the individual state vector, but belongs to a larger state space. An entangled state of two spin ½ particles is the following:
. (This cannot be done if Sx and Sz are measured on the same particle, since Sx and Sz are incompatible observables.) In general, however, once two quantum systems have interacted, they become correlated in such a way that measurement results can no longer be anticipated by just assigning an individual state vector to each partner. Instead, a unique, global state vector has to be associated to the whole pair. This state is constructed by combining the individual state vector, but belongs to a larger state space. An entangled state of two spin ½ particles is the following:
The statistical predictions associated with ![]() are very important. The probability of finding ‘up' or ‘down' if Sz (or any other spin component) is measured on each particle separately is 1/2. Furthermore, if one of the particles is found having spin ‘up' in the z direction, the result of any spin measurement carried out subsequently on the other particle will follow the statistics predicted by
are very important. The probability of finding ‘up' or ‘down' if Sz (or any other spin component) is measured on each particle separately is 1/2. Furthermore, if one of the particles is found having spin ‘up' in the z direction, the result of any spin measurement carried out subsequently on the other particle will follow the statistics predicted by ![]() ; if, conversely, the first particle is found having spin ‘down' in the z direction, then the statistics of the other particle will be that corresponding to
; if, conversely, the first particle is found having spin ‘down' in the z direction, then the statistics of the other particle will be that corresponding to ![]() . Due to the peculiar form of state (4), analogous correlations exist for any direction in space. Thus, if, for example, particle 1 is found to have spin ‘up' in the x direction, particle 2 will follow the predictions of
. Due to the peculiar form of state (4), analogous correlations exist for any direction in space. Thus, if, for example, particle 1 is found to have spin ‘up' in the x direction, particle 2 will follow the predictions of ![]() ; and so on (the situation is represented in figure 4). Indeed,
; and so on (the situation is represented in figure 4). Indeed, ![]() preserves its mathematical form if expressed in terms of the eigenvectors of Sx:
preserves its mathematical form if expressed in terms of the eigenvectors of Sx:
![]() .
.
The probability distributions observed in measurements addressing a single particle are fundamentally different depending on whether the particle has or has not an entangled partner. In the former case, as shown by figure 8, interference effects are washed out (this can readily be derived from the above definition of ![]() by using formulas (3); see also complementarity).
by using formulas (3); see also complementarity).
An important corollary of rules I-III is the following: the state vector ![]() which corresponds to the special case in which we can predict with certainty (i.e. with probability 1) that the measurement of A will yield the value
which corresponds to the special case in which we can predict with certainty (i.e. with probability 1) that the measurement of A will yield the value ![]() is the unit vector lying on the
is the unit vector lying on the ![]() axis (
axis ( ![]() ). Following Dirac's notation, this vector is denoted
). Following Dirac's notation, this vector is denoted ![]() and is called an eigenstate (or eigenvector) of A.
and is called an eigenstate (or eigenvector) of A.
Let's apply these simple rules to the Stern-Gerlach experiments discussed in the section on experimental evidence. We are concerned with two spin observables: Sz, which can take the two ‘values' ![]() and
and ![]() ; and Sx, which can take the two ‘values'
; and Sx, which can take the two ‘values' ![]() and
and ![]() . In the first step of the experiment (figure 2) only those atoms are selected for which a measurement of Sz yields
. In the first step of the experiment (figure 2) only those atoms are selected for which a measurement of Sz yields ![]() . For these atoms, we have the certainty of finding
. For these atoms, we have the certainty of finding ![]() if the measurement of Sz is repeated. Therefore, the associated state vector is
if the measurement of Sz is repeated. Therefore, the associated state vector is ![]() . If, on the sample of atoms thus prepared, we now measure Sx, we find
. If, on the sample of atoms thus prepared, we now measure Sx, we find ![]() for half of the atoms and
for half of the atoms and ![]() for the other half (step 2 of figure 3). Can this result be represented in our state space? Yes, it is sufficient to take the two axes corresponding to
for the other half (step 2 of figure 3). Can this result be represented in our state space? Yes, it is sufficient to take the two axes corresponding to ![]() and
and ![]() (see rule I) as forming an angle of p/4 with the axes corresponding to
(see rule I) as forming an angle of p/4 with the axes corresponding to ![]() and
and ![]() (figure 6a). According to rule III, to calculate the probability of finding
(figure 6a). According to rule III, to calculate the probability of finding ![]() we have to project the state vector
we have to project the state vector ![]() on the axis corresponding to
on the axis corresponding to ![]() (figure 6a). In the same way we calculate the probability that the measurement of Sx yields
(figure 6a). In the same way we calculate the probability that the measurement of Sx yields ![]() . We get:
. We get:
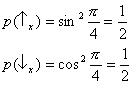
The result of the third experiment (figure 3) can be straightforwardly formalised in the same way, observing that the first two apparatuses ‘prepare' the state ![]() (figure 6b).
(figure 6b).
Let's see how interference phenomena are taken into account by this simple model. Exploiting the elementary rules for the composition of vectors in the plan, the vectors ![]() and
and ![]() can be rewritten as follows:
can be rewritten as follows:
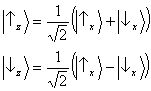
Notice that both these states predict the same probability distribution for a measurement of Sx: ![]() . Therefore, the two states (or, to be more precise, the corresponding preparations) cannot be distinguished a posteriori by performing such a measurement. The two preparations yield however opposite statistical results if a measurement of Sz is carried out (figure 7). In the former case one always finds ‘
. Therefore, the two states (or, to be more precise, the corresponding preparations) cannot be distinguished a posteriori by performing such a measurement. The two preparations yield however opposite statistical results if a measurement of Sz is carried out (figure 7). In the former case one always finds ‘ ![]() ' ; whereas in the latter, this never happens. This ‘never' is the signature of interference (compare to the bright and dark fringes of the double-slit experiment). Notice that the only mathematical difference between the two states (3) is the sign of the superposition: plus in the former case, minus in the latter. This sign expresses the phase relation existing between
' ; whereas in the latter, this never happens. This ‘never' is the signature of interference (compare to the bright and dark fringes of the double-slit experiment). Notice that the only mathematical difference between the two states (3) is the sign of the superposition: plus in the former case, minus in the latter. This sign expresses the phase relation existing between ![]() and
and ![]() . (Using complex notation,
. (Using complex notation, ![]() or
or ![]() depending on whether j = 0 or j = p; it's worth to make a comparison with waves.)
depending on whether j = 0 or j = p; it's worth to make a comparison with waves.)


