
The formal tool allowing one to account both for the corpuscular and wavelike aspects of quantum phenomena is the wave function (introduced by Erwin Schrödinger in 1926, together with the famous equation governing its time evolution). It associates to any position in space and time ![]() a complex number
a complex number ![]() , called probability amplitude.
, called probability amplitude. ![]() contains part of the information encoded in the system's quantum state, and allows one to calculate the probability associated with the possible outcomes of measurements involving kinematical variables such as position and momentum. The modulus squared of the wave function,
contains part of the information encoded in the system's quantum state, and allows one to calculate the probability associated with the possible outcomes of measurements involving kinematical variables such as position and momentum. The modulus squared of the wave function, ![]() , gives for example the probability of finding the system in
, gives for example the probability of finding the system in ![]() at instant t (this important result can be derived from Born rule). According to de Broglie relations, the wave function associated with a beam of atoms with equal momentum p and energy E, is a monochromatic wave of wavelength l = h/p and frequency n = E/h. For instance, a spherical wave provides a good approximation of the wave function associated with an atom propagating from a point-like source:
at instant t (this important result can be derived from Born rule). According to de Broglie relations, the wave function associated with a beam of atoms with equal momentum p and energy E, is a monochromatic wave of wavelength l = h/p and frequency n = E/h. For instance, a spherical wave provides a good approximation of the wave function associated with an atom propagating from a point-like source:
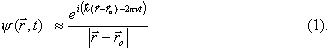
( ![]() being the position of the source,
being the position of the source, ![]() being the wave vector governing the propagation of the wave, whose modulus is 2p/l). Notice that in this example
being the wave vector governing the propagation of the wave, whose modulus is 2p/l). Notice that in this example ![]() is significantly different from zero over a large region of space. This means that the probability distribution associated with the possible detection of the atom is completely delocalised. Well-localised particles (i.e. particle behaving as corpuscular objects) are not associated with a monochromatic wave but rather with a wave packet. Wave packets can be regarded as superpositions of an infinite number of monochromatic waves of different wavelengths, interfering destructively anywhere but in a small region where they add up constructively giving rise to a signal. The spectral and spatial extensions of a wave packet have to obey uncertainty relations.
is significantly different from zero over a large region of space. This means that the probability distribution associated with the possible detection of the atom is completely delocalised. Well-localised particles (i.e. particle behaving as corpuscular objects) are not associated with a monochromatic wave but rather with a wave packet. Wave packets can be regarded as superpositions of an infinite number of monochromatic waves of different wavelengths, interfering destructively anywhere but in a small region where they add up constructively giving rise to a signal. The spectral and spatial extensions of a wave packet have to obey uncertainty relations.
The interference pattern observed in the double-slit experiment is easily understood in terms of wave function. For the two slits split the wave associated with the incoming atom beam into two secondary spherical waves ![]() and
and ![]() (like in figure 3). The atom's wave function
(like in figure 3). The atom's wave function ![]() after the double-slit filter is given by a weighted sum of these two secondary waves. This is why an ensemble of atoms produces interference fringes on the detection plate: the maxima and minima of probability reflect precisely the different phase relations existing at different points of the detection screen between the two waves
after the double-slit filter is given by a weighted sum of these two secondary waves. This is why an ensemble of atoms produces interference fringes on the detection plate: the maxima and minima of probability reflect precisely the different phase relations existing at different points of the detection screen between the two waves ![]() and
and ![]() (see figure 2 and the related discussion).
(see figure 2 and the related discussion).
In general, however, whether an ensemble of systems does or does not display interference is not a matter of size. Rather, it depends on the amount of information in principle available to the observer. To make this point clear, let's go back to the double-slit experiment and work out explicitly the probability p(x) of detecting an atom at a point of longitude x. Following an approach due to Richard Feynman, we consider the two possible ‘paths' connecting the atom source to each point of the detection screen (see figure 9). We will call the paths coming from slit 1: '↑' paths, and the paths coming from slit 2: ‘↓' paths.
• Case 1 – INDISTINGUISHABLE PATHS
Suppose that there is no way - neither in principle - to know if the atom has followed a '↑' path or a ‘↓' path (the paths are said in this case to be indistinguishable). The state vector representing this situation is the following:
Applying Born rule to state (2) one can formally derive the spatial distribution p(x) expected in this case. Our previous discussion on wave functions provides us with the recipe necessary to carry out this simple calculation. We get:
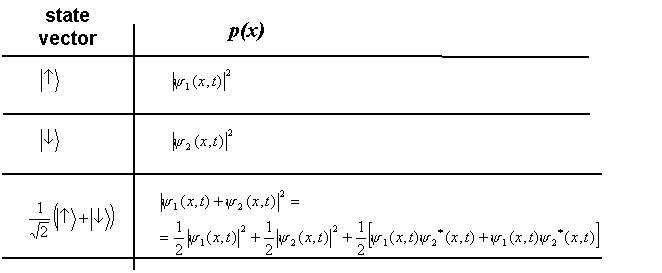
![]() and
and ![]() correspond respectively to the red and blue distributions in figure 5. Besides the weighed sum of these two terms (green curve A in figure 5), the probability associated with state (2) contains ‘cross' terms. It is easily seen using eq. (1) that cross terms oscillate as a function of x. Added to the first and second term, this oscillating function produces the typical interference pattern (green curve B in figure 5).
correspond respectively to the red and blue distributions in figure 5. Besides the weighed sum of these two terms (green curve A in figure 5), the probability associated with state (2) contains ‘cross' terms. It is easily seen using eq. (1) that cross terms oscillate as a function of x. Added to the first and second term, this oscillating function produces the typical interference pattern (green curve B in figure 5).
• Case 2 – DISTINGUISHABLE PATHS
Let's consider now the case in which the experimental set-up is equipped to discriminate the paths (without disturbing the motion of the atoms). Suppose for example that the atoms are excited and decay emitting a photon exactly while passing through the slit (figure 6). Detecting the emitted photon would bring to our knowledge the ‘which slit' information. Therefore, ‘↑' paths and ‘↓' paths are now distinguishable (in the sense that they can – in principle – be distinguished). Let W be the photon observable carrying the ‘which slit' information, and let's call conventionally ‘ ![]() ' the outcome of W indicating slit 1 and ‘
' the outcome of W indicating slit 1 and ‘ ![]() ' the outcome of W indicating slit 2. The state vector corresponding to the new experimental configuration is the following entangled state, involving the atom and the emitted photon:
' the outcome of W indicating slit 2. The state vector corresponding to the new experimental configuration is the following entangled state, involving the atom and the emitted photon:
According to the definition of entangled state, if the photon indicates ![]() , then the corresponding atom will follow the probability distributions predicted by state
, then the corresponding atom will follow the probability distributions predicted by state ![]() , while if the photon indicates
, while if the photon indicates ![]() , then the corresponding atom will follow the probability distributions predicted by
, then the corresponding atom will follow the probability distributions predicted by ![]() . Since each photon indicates either
. Since each photon indicates either ![]() or
or ![]() (there is not a third possibility), it's clear that each atom is compelled to follow either the spatial distribution associated to
(there is not a third possibility), it's clear that each atom is compelled to follow either the spatial distribution associated to ![]() or the one associated to
or the one associated to ![]() . Therefore, if we look at the detected atoms disregarding the information supplied by the photon, we will see a spatial distribution that is simply the weighted sum of the probability distributions predicted by
. Therefore, if we look at the detected atoms disregarding the information supplied by the photon, we will see a spatial distribution that is simply the weighted sum of the probability distributions predicted by ![]() and
and ![]() . The weights of the sum are the probabilities for the outcomes
. The weights of the sum are the probabilities for the outcomes ![]() and
and ![]() to occur, i.e. 1/2 and 1/2.
to occur, i.e. 1/2 and 1/2.
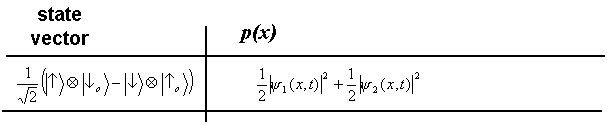
Cross terms, and therefore interference fringes, are here absent (compare to the discussion on the entangled states of spin ½ particle).
The disappearance of interference when the ‘which slit' information becomes in principle available should not appear too surprising. The atom state vectors ![]() and
and ![]() can be expressed as superpositions of either position eigenstates or momentum eigenstates. Therefore, they assign probabilities not only to position but also to momentum values. In particular, state
can be expressed as superpositions of either position eigenstates or momentum eigenstates. Therefore, they assign probabilities not only to position but also to momentum values. In particular, state ![]() assigns probability 0 to momenta indicating that ‘the atom is coming from slit 2', whereas the opposite is true for
assigns probability 0 to momenta indicating that ‘the atom is coming from slit 2', whereas the opposite is true for ![]() . Thus , making the ‘which slit' information available amounts to (partially) measure the atoms' momentum. Position and momentum being incompatible observables, a measurement of momentum unavoidably modifies the spatial distribution of the atoms in any further measurement of position. Interference, in particular, is washed out (see the discussion of quantum states for more details).
. Thus , making the ‘which slit' information available amounts to (partially) measure the atoms' momentum. Position and momentum being incompatible observables, a measurement of momentum unavoidably modifies the spatial distribution of the atoms in any further measurement of position. Interference, in particular, is washed out (see the discussion of quantum states for more details).
Feynman's rules are a powerful tool that can be used in several contexts, once a set of ‘paths' and the corresponding probability amplitudes have been recognised. Interference itself is a very general feature of quantum phenomena, not limited to position measurements. Regardless of the way in which a system is prepared, one can always find an observable such that the probability distributions associated with its outcomes displays interference (meaning that some outcomes are found with high probability while others are never found). In general, if the state of the system can be written as a superposition of the eigenstates of an observable A, interference fringes are seen when measuring an observable B incompatible with A. The condition for interference to be observed is that there is no ‘which path' information available (neither in principle), i.e. that there is no observable C which has outcomes that are correlated with those of the ‘path observable' A (see the example of spin observables).
Interference effects illustrate the deep connection between the principle of superposition, incompatible observables and complementarity. This link shows in turn to what extent the mathematical core of quantum theory is determined by the relations existing among the observables we use to ‘structure' physical phenomena (see implications).


